Th : f : Gà G’ morph de groupes

H ss gpe de G Þ f(H) ss gpe de G’

H’ ss gpe de G’ Þ f^-1(H’) ss gpe de G

Congruences : aº b [n] Û (a-b) multiple de n

aº b [n] Û a et b ont même reste par div eucl par n

congruence [n] : rel d’équiv sur Z, Cl(a)={bÎ Z, aº b [n]}={...,(a-2n),(a-n),a,(a+n),(a+2n),...}

elle est compatible avec + et x

Z/nZ ={classes de n entiers consécutifs}

Cl(a)+Cl(a’)=Cl(a+a’) Cl(a).Cl(a’)=Cl(a.a’)

Th : (Z/nZ,+) gpe abélien d’élément neutre Cl(0)

Th : f : Zà G (G,.) gpe aÎ G

nà aⁿ morphisme de groupes

Def : (G,.), aÎ G, les puissances de a sont le ss gpe engendré par a : Gr(a)

H ss gpe de G si $ aÎ G | H=Gr(a) alors H monogène et cyclique si H fini

Th : Cl(n’) engendre Z/nZ Û n et n’ 1^ers entre-eux

Ordre de a : card du ss gpe qu’il engendre

Action de G sur E : GxEà E

(g,x)à g*x

tq " (g,g’)Î G², " xÎ E, g*(g’*x)=(g.g’)*x

" xÎ E, e*x=x

Orbite : Orb (x)=G ;x={yÎ E, $ gÎ G | y=g*x} xÎ Orb(x), ens des orbites sous action de G : partition de E

Caract idéaux : A anneau commutatif, IÌ A, I idéal de A Û (I¹ Æ " (x,y)Î I², (x+y)Î I " xÎ I, " aÎ A,axÎ I)

Th : f morph Aà A’, si I idéal de A alors f(I) n’est pas un idéal de A’

si I’ idéal de A’ alors f^-1(I’) est un idéal de A

petit th de Fermat : si p premier, " nÎ Z, n^pº n [p]

Dans Z, idéaux de Z : ss gpes nZ, nÎ N Z anneau principal

f : K[X]à A

Pà P(a ) morph. d’algèbre

Polynôme annulateur : Ker f={PÎ K[X], P(a )=0} idéal de K[X]

Th : si a admet un polyn min Pa de deg n alors K[a ] de dim n et (a ⁰,a ¹,...,a ⁿ) base.

Projecteurs : p o p=p

Im(p) invariant par p, E=Im p Å Ker p, p proj sur Im(p) et (Id-p) proj sur Ker(p)

Matrices : Tr(AB)=Tr(BA) Tr(^tA)=Tr(A)

Matrices semblables : B=P^-1AP PÎ GL_n(K)

équivalentes : B=PAQ PÎ GL_n(K) QÎ GL_n(K)

Dualité : E ev sur K

Esp. Dual de E sur K noté E* : ens des formes linéaires sur E E*=L(E,K)

Si F admet un supplémentaire G de dim finie, alors tous les supplem. de F sont isomorphes à G de dim codim(F)

gof=0 Û Im f Ì Ker g

Ker f Ì Ker(gof) Im(gof) Ì Im g Ker f^nÌ Ker fⁿ⁺¹ Im f^n+1Ì Im fⁿ

Th : E ev, H hyperplan, $ j forme linéaire tq Ker(j )=H

Def : B=(e₁,e₂,...,e_n) base de E

Formes coordonnées : (j _{1,j 2,...,j n}) tq j _i : Eà K xà coord n°i de x dans B

Ces formes constituent une base de E*

Th : (e₁...e_p) vect de E, u : E*à K^p associé, (e_1...e_p) libre Û u surjective

u : j à (j (e₁),j (e₂),...,j (e_n))

Th : (j _{1...j p}) formes lin, v : Eà K^p associé, (j _{1...j p}) libre Û v surjective

j forme bilin sym, q(x)= j (x,x) q(x+y)=q(x)+q(y)+2j (x,y) q(l x)=l ²q(x)

Def : Forme quadratique q : Eà R Û j (x,y)=1/2*(q(x+y)-q(x)-q(y)) q(l x)=l ²q(x)

j et q sont positives si " xÎ E, q(x)³ 0

j et q def positives Û elles sont positives et " xÎ E, q(x)= j (x,x)=0 Þ x=0

On a alors égalité dans l’inégalité de Cauchy

Th : A la matrice de j et q dans B base, (x,y)Î E², X et Y leur mat colonne dans B

j (x,y)=^tXAY q(x)=^tXAX

Matrices congruentes : A et B congruentes Û B=^tPAP (P inversible), les matr ont même rang et un det de même signe.

Méthode de Gauss : on forme des carrés.

Def : base q-orthogonale de E : base ou q s’exprime par cad une base dans laquelle M(q) est diag.

Th : Toute forme quadratique admet des bases de réduction

q forme quadratique de rang r¹ 0,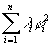

décomp en carrés de q

p : nb de coef l >0 et p’ : nb de coef l <0 sont indep de la décomp effectuée

Def : signature de q : couple (p,p’)