" n Î Z, $ ! kÎ N, $ ! (p1,p2,...,pm)Î Pm, $ ! (a 1,a 2,..a n)Î (N*)k, $ ! e Î {-1,1} |
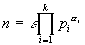
à Arithmétique dans Z :
" (a,b,c)Î Z3, a|b et a|c Þ a|(b+c) a|b Þ a|bc
nombre premier : nb p³ 2, divisible dans N par p et 1 seulement.
Th. d’Euclide : P (ensemble de nombres premiers) est infini
| Th. de décomposition en facteurs premiers :
" n Î Z, $ ! kÎ N, $ ! (p1,p2,...,pm)Î Pm, $ ! (a 1,a 2,..a n)Î (N*)k, $ ! e Î {-1,1} | |
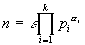 |
Valuation d’un nb premier dans un entier : nb d’occurrences de p dans décomposition en facteurs premiers.
| PGCD(m,n) = | 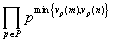 |
PPCM(m,n) = | 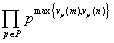 |
k diviseur commun de m et n Û k|(m Ù n)
k multiple commun de m et n Û (m v n)|k
Algorithme d’Euclide :
a, b entiers naturels, r0, r1, ... tq r0=a, r1=b et r2=reste division eucl de r0 par r1
etc ...
$ n0 | r(n0)=0 et r(no-1)= a Ù b
Th de Bezout : (a,b)Î (N*)², $ (u,v)Î Z² | au+bv=a Ù b
Th. de Gauss :
" (a,b,c)Î (Z*)3, a|bc et a Ù b=1 Þ a|c
à Polynômes :
S0(K) : ens des suites à coef. Dans K, stationnaires en 0.
(S0(K),+,x,*) algèbre sur K
d°(A(X)+B(X))£ Max(d°(A),d°(B))
d°(AB)=d°(A)+d°(B)
Division euclidienne : A(X) et B(X) 2 polynômes
$ ! (Q(X), R(X)) polyn. tq A(X)=B(X)Q(X)+R(X) et d°(R(X)) £ d°(B(X))
Polyn assoc. : (A|B et B|A) ou (A=uB) Û A et B associés
Polyn normalisé : polyn. dont le coef. de + haut d° est 1.
è mêmes propriétés que pour arithmétique dans Z
Th. de décomposition en facteurs premiers : " aÎ (K[X])*,$ mÎ B,$ uÎ K*,
| $ (P1,P2,...,Pm)Î (K[X])m, tq A= | 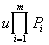 |
avec Pi irréductible et normalisé |
Polynômes scindé : Tous les polynômes de sa décomposition sont irréductibles et du 1er degré.
Pà Fp est un isomorphisme d’algèbre de K[X] dans A(K,K)
Th. de Bézout, Gauss, Taylor ...
Ordre de multiplicité : Op(a)=Max {kÎ N | (X-a)k|P(X)}
Th. de d’Alembert-Gauss : Tout polyn. de C[X] de d° ³ 1 a au moins une racine dans C.
Application polynomiale symétrique fondamentale : s k(x1,...,xn)=S Xi1...Xik avec 1£ i<...<ik£ n
Th. relation coef-racines : P scindé de coef. a0...an, de racines x1...xn
| alors " kÎ [[1,n]], on a : | 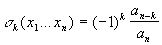 |