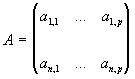
à Matrices :
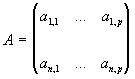 |
matrice à n lignes et p colonnes. |
t.g. (terme générique), terme a(i,j) situé à la i ième ligne et à la j ième colonne.
Ensemble des matrices : M(n,p)(K)
M(Be,Bf)(f)=M(Bf)(f(Be))
Matrice élémentaire(i,j) : matrice avec que des 0 sauf au terme (i,j) où on a un 1, de t.g. d (i,i0)*d (j,j0).
Produit matriciel et par blocs
M(Bf)(f(S))=M(Be,Bf)(f)*M(Be)(S)
M(gof)=M(g)*M(f)
Une matrice M(n,n) est inversible si $ M’ | MM’=In
A matrice, tA est une matrice de t.g. a’(i,j)=a(j,i)
t(AB)=tBtA
AÎ GLn(K) Û tAÎ GLn(K) et dans ce cas t(A-1)=(tA)-1.
A est symétrique si tA=A et antisymétrique si tA=-A
Matrices triangulaires supérieures si " (i,j)Î [[1,n]]², i>j Þ a(i,j)=0 (inférieures ...)
Matrice diagonale si " (i,j)Î [[1,n]]², i¹ j Þ a(i,j)=0 dans ce cas le produit matriciel est le produit terme à terme.
Matrices scalaires : l In
à Changement de base :
Th. : M(B)(S)=M(B)(B’)*M(B’)(S)
M(B)(B’) : matrice de passage de B à B’ :P(B,B’)
Elles sont transitives, (P(B,B’))-1=P(B’,B)
Chgmt de bases pour les applic. lin. : M(B’e,B’f)(f)=(P(Bf,B’f))-1*M(Be,Bf)(f)*P(Be,B’e)
è La trace ne dépend pas de la base choisie.
Soit p une proj. de matrice M alors dim(E1)=rg(p)=Tr(M)
Calcul d’inverse de matrice : On transforme en système entre les nouvelles et les anciennes coordonnées, les coef. de chaque ligne sont pris en colonne dans la matrice.
à Rang, équivalences des matrices :
rg(S)=dim(Vect(S))
rg(f)=dim(Im(f))=rg(f(Be))
Sc : syst. des vecteurs colonnes d’une matrice
Sl : syst. des vecteurs lignes d’une matrice
rg(M)=rg(Sc(M))
Matrice type de rang r : matrice nulle sauf des 1 sur les r premières valeurs de la diagonale
équivalence de matrices : M~N Û $ (P,Q)Î GLn(K)*GLp(K) | M=PNQ
M~N Û rg(M)=rg(N)
Manipulations élémentaires (réversibles).
On ne change pas le rang d’une matrice en effectuant des manip. élémentaires.
MÎ GLn(K) Û rg(M)=n Û M~In
MÎ GLn(K) Û on peut, par manip. elem. sur les lignes seulement, tansformer M en In
On obtient M-1 en effectuant les mêmes manip. sur In.
à Déterminants :
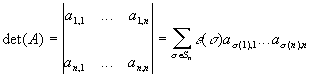 (n! termes)
(n! termes)
si det d’ordre 3 à Règle de Sarrus
Th. : det(tA)=det(A)
n-linéairité : f : E1xE2x...xEnà F est n-linéaire si linéaire pour toutes les applic. partielles.
f est symétrique : " (x1,...,xn)e En, " s de [[1,n]], f(x(s (1)),...x(s (n)))=f(x1,...,xn)
antisym. ou alternée s’il y a un signe -
f alternée Û f(x1,...,xn)=0
Th. : l’applic. det(B) est l’unique f forme n-lin. alternée sur E tq f(B)=1
det(B’)(B)=1/(det(B)(B’)
Th. d’orientation : R : BRB’ Û det(B)(B’)>0 relation d’équiv. Qui partage B en 2 classes d’équiv.
Th. : det(MM’)=det(M)*det(M’)
det(fog)=det(f)*det(g)=det(gof)
Développement par rapport à une ligne ou une colonne (Ne pas oublier le signe - éventuel).
Matrice mineure de A : matr carrée de taille (n-1) ou on a enlevé la i ieme ligne et la j ieme colonne
Un cofacteur est le det d’une matrice mineure.
Rq : Si on échange 2 lignes ou colonnes, le det est * par -1 (plus galement : e (s ) )
Si 2 lignes sont proportionnelles : det = 0
Si il y a une ligne ou colonne formée de 0 : det = 0
Mais, on ne change pas le det en ajoutant une c.l. des autres lignes à une ligne (ou colonne).
Det d’une matrice triangulaire : produit des termes de la diagonale (valable pour det par blocs).
Th. : A*t com A= t com A*A=det(A)In
A-1=1/det(a)*t com A