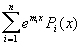
à Equations différentielles :
a, b, c 3 fonctions définies sur I à valeurs dans K, continues
Pour trouver y0 : y0=exp(-A(x)) où A primitive de b/a sur I, Þ ln(y0(x))=-A(x) Þ y’0(x)/y0(x)=-b(x)/a(x) Þ a(x).y’0+b(x).y0(x)=0.
Pour trouver une SP, on écrit :
y=Cy0 (*b)
y’=Cy0’+C’y0 (*a)
2ème mb=0+C’y0 on trouve C’ puis C
Raccordements des points non définis
Eq. diff du 2ème ordre
Soit y1 une SP de (E) alors S={y1+l y0+m z0, (l ,m )Î K²}
Résolution de (e) :ay’’+by’+c=0 on résout l’eq caractéristique ar²+br+c=0
Dans R, on a :
D <0 : sol a +ib et a -ib alors sol xà exp(a x)(l cos (b x)+m sin (b x))
D =0 : xà exp(r0x)(l x+m )
D >0 : xà l exp(r1x)+m exp(r2x)
Recherche de la Solution Particulière :
| ay''+by'+cy= | 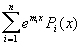 |
n=1 : si m n’est pas sol de l’EC : sol du type exp(mx)Q(x) avec Q de même degré que P
si m est sol simple : sol : x Q(x) exp(mx)
si m est sol double : sol : x² Q(x) exp(mx)
n qcq : on superpose les solutions
Rq : si sin ou cos, on superpose les sol. ...
à Intégration sur un intervalle quelconque :
s(I)={segments inclus dans I}
f est intégrable sur I si {ò f sur J, JÎ s(I)} est majoré, alors c’est la borne Sup.
f int sur [a,b[ Û ]a,b[à R, xà ò f(t) dt a une lim en b-
Chasles
f+g int. Û f et g int. f~g f int. Û g int.
ex fondamentaux : 1/(b-x)a int. sur [a,b[ Û a <1
fa (x)=1/xa int sur [1,+¥ [ Û a > 1 1/(x-a)a int sur ]a,b] Û a <1 ...
f +=Sup (f, 0) f -=Sup (-f, 0)
f int si f + et f - int et alors ò f=ò f + - ò f -.
f int sur I Û |f| int sur I et alors |ò f| £ ò |f|
prop de l’intégrale de Riemann qui se généralisent : linéarité, conjugaison, stricte croissance pour les fonctions continues, ineg. de Schwarz ...
Pratique de l’étude :
à Fonctions de deux variables :
norme eucl ![]() infinie
infinie ![]()
partie bornée : AÌ R² est borné si $ k>0 | AÌ D°(O,k)
W partie ouverte si " M0Î W , $ e >0 | D°(M0,e ) Ì W
partie fermée, complémentaire d’une partie ouverte
M adhérent à D si $ P=(Pn)(nÎ N) de DN qui converge vers M0
applic. projection (x,y)à x et (x,y)à y
Eq. d’ouverts : {MÎ R² | f(M)>0} on remplace par ³ ou = pour eq. de fermé.
Dérivabilité :
f derivable en M0 dans la direction de H :
![]()
f(M0+h)=f(M0)+h ¶ f/¶ x(m0)+k ¶ f/¶ y(M0)+||H|| e (M0+H)
![]()
f(M0+H)-f(M0)=grad (f)(M0).H+ ||H|| e (M0+H)
Th. de Schwarz : f de cl C2 sur ouvert U de RN, ¶ ²f/(¶ x¶ y)=¶ ²f/(¶ y¶ x)
Th. des fct implicites :
f(M0)=0 ¶ f/¶ y(M0)¹ 0
f(x,y)=0 Û y=j (x)
à Intégrales doubles :
On commence par les fonctions en escalier ...
ò ò f=ò ò f(x,y) dx dy
Linéarité, " Chasles " ...
| Th. de Fubini : ò ò f (sur R)= | 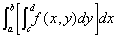 |
où R=[a,b]x[c,d] |
On applique le même type de raisonnement que pour l’intégration simple
On peut généraliser à des domaines simples (pas forcément rectangulaires).
Th. de chgmt de variable :