à
Relations binaires : Soit R une relation binaire. Elle est :relation d’ordre : réflexive, antisymétrique, transitive
relation d’équivalence : réflexive, symétrique, transitive
à
Structures :L
oi de composition interne : définie de ExE sur E"
(x,y,z)Î E3, soit V une l.c.i.Monoïde : E muni d’une loi associative et ayant un neutre (commutatif Si loi commutative)
Groupe : G tq G monoïde et symétrisé (abélien si commutatif)
Anneau : A muni de 2 lois + et * tq (A,+) groupe abélien
associative, distributive/+, munie d’un neutre (commutatif avec * commutative)
anneau intègre : commutatif tq
" (a,b)Î A², a*b=0 Þ (a=0 ou b=0)A°: ensemble des éléments inversibles de A.
Corps : anneau commutatif tq 0
¹ 1 (c’est un anneau intègre où tous les éléments ¹ 0 sont inversibles)à
Ensembles finis :Toute partie non vide de N a un plus petit élément.
E, F 2 ensembles de cardinal p et n : L’ensemble des applications E dans F est de card n^p
L’ensemble des injection de E dans F est de card n!/(n-p)!
L’ensemble des bijections de E dans F est de card n!
Arrangements : A(n,p) = n!/(n-p)!
Combinaison : nb de parties à p él. : C(n,p) = n!/(p!(n-p)!)
![]()
Th. du binôme de Newton :
![]()
à
Les réels :S est le sup si c’est le plus petit el. des majorants de A
M=Max(a) Û (M=Sup(A) et MÎ A)
Q est dense dans R : " (a,b)Î E², a<b, $ rÎ Q | a<r<b
+
Valeurs absolues : x²=y² Û |x|=|y| Û x=y ou x=-y| |x|-|y| |
£ |x+y| £ |x|+|y||xy| = |x| |y|
C est convexe dans R si
" (a,b)Î C², a£ b Þ [a,b]Ì Cà
Les complexes :exp(iq )=cos q +i sin q
exp(iq )^n=exp(inq )
arg(zz’)=arg(z)+arg(z’)
arg (1/z)=-arg (z)
U : ens des complexes de module 1
Exp complexe : exp(z)=exp(a)exp(ib)=exp(a)(cosb+isinb) avec z=a+ib
La restriction de exp à {a+ib (a,b)Î Rx[a ,a +2p ]} est bij. sur C*
Recherche des racines carrées : Z=A+iB z=a+ib racine de Z
a²=(A+Ö (A²+B²))/2 b²=-(A+Ö (A²+B²))/2
ex : racine de 5+12i a²-b²=5 2ab=12 ...
| Linéarisation : cosmx sinnx = | 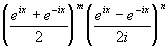 |
Délinéarisation : cos (px)=Re(exp(ipx)) de même pour sin ...
| cos(px) = | 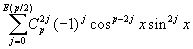 |
| sin(px) = | 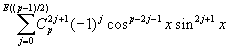 |
1+x+x²+ ... +xn-1=(xn-1)/(x-1) avec x ¹ 1 (suites géométriques)
Un={exp(i2kp /n ; kÎ Z}