Système libre :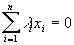

Þ " iÎ [[1,n]], l i=0

un système est lié Û un de ces éléments est une c.l. des autres

Vect (A) : ens des c.l. de A

L’intersection de 2 ss ev est un ss ev

F1, F2 2 ss ev : l’ens. {x1+x2, (x1,x2)Î F1xF2} est un ss ev de E

2 ss ev sont supplémentaires si F1Ç F2={0} et F1 Å F2=E

un système est générateur de E si " xÎ E, x est c.l. du système.

Un système libre et générateur est une base.

Toutes les bases d’un même ev ont le même nombre d’éléments.

Si S est libre et p=n Þ S est une base

Th. : On peut toujours compléter un système libre en une base.

FÌ G (2 ss ev) et dim(F)=dim(G) Þ F=G

Grassmann : F et G 2 ss ev de dim finie alors F+G est de dim finie et dim(F+G)=dim(F)+dim(G)-dim(FÇ G)

FÇ G={0} F+G=E dim(F)+dim(G)=dim (E)

2 de ces 3 propriétés suffisent pour que F Å G=E

à Applications linéaires : (Ö homomorphismes)

" (x,y)Î E², f(x+y)=f(x)+f(y) et " (l ,x)Î KxE, f(l x)=l f(x)

caractérisation : conservation des c.l.

ens : L(E,F)

B base de E de dim n, fÎ L(E,F) alors f inj. Û f(B) libre

f surj. Û f(B) générateur de F

" (f,g)Î (L(E,F))², f+gÎ L(E,F) et Im(f+g)Ì Im(f)+Im(g)

Ker(l f)=Ker(f) et Im(l f)=Im(f)

Munie de ses 3 opérations, L(E) est une K-algèbre, non commutative, non intègre (sauf si E de dim finie=0 ou 1)

Groupe GL(E) : ens. des automorphismes.

Ex d’endomorphismes :

les homothéties : hl =l Ide

elles commutent avec tous les endomorphismes.

Les projections : E1, E2 sont 2 ss ev supplémentaires dans E

" xÎ E, $ ! (x1,x2)Î E1xE2 | x=x1+x2

f proj. de x sur E1 parallèlement à E2 alors f(x)=x1 (de même pour x2 sur E2 ...)

Ker(f)=E2 et Im(f)=E1

caract. : pop=p

p et q 2 proj. assoc. Û p+q=Ide et poq=qop=0

caract. : sos=Ide

E est un K-ev de dim finie et fÎ L(E) : f inj Û f surj Û f automorphisme.

Forme linéaire : applic. linéaire Eà K avec sa structure d’ev sur lui même

dual : E*=L(E,K)

B=(e1...en) base de E,(l 1,...l n) les coord de x dans B, xà l i sont des formes lin. notées (e1*,...en*)

" (i,j)Î [[1,n]]², ei*(ej)=d (i,j)