f est sym si " (x,y)Î E², f(x,y)=f(y,x)

Produit scalaire : forme bilin, sym, def positive (" xÎ E, f(x,x) ³ 0 et f(x,x)=0 Û x=0)

ex : f((x,y),(x’,y’))=xx’+yy’

Norme assoc : ||x||=Ö (<x|x>)

ineg. de Schwarz : |<x|y>| £ ||x||.||y||

ineg. de Minkowski : | ||x||-||y|| | £ ||x+y|| £ ||x||+||y||

d(M,N)=||MN||

formule de polarisation : <x|y> = ¼(||x+y||²-||x-y||²) identité du parallélogramme : ||x+y||²+||x-y||²=2(||x||²+||y||²)

u et v orthogonaux si <x|y>=0

Th. de Pythagore : u^ v Û ||u+v||²=||u||²+||v||²

qq propriétés : A^ B Û AÌ B^ Û BÌ A^ AÌ B Û B^ Ì A ...

syst. orthog " (i,j)Î I², i¹ j, ui^ uj orthonormé : orthog. Et " iÎ I, ||ui||=1

cad " (i,j)Î I², <ui|uj>=d (i,j)

Tout syst orthonormé est libre.

Procédé de Schmidt pour trouver une b.o.n. de E

on pose u1=e1/||e1||

u’2=e2-<e2|u1>u1 puis u2=u’2/||u’2||

u’3=e3-<e3|u1>u1-<e3|u2>u2 puis u3=u’3/||u’3||

etc ...

F et F^ sont supplémentaires.

f est sym. si <f(x)|y>=<x|f(y)> et antisym. si <f(x)|y>=-<x|f(y)>

f sym Û M(B)(f) est sym (resp. antisym.)

Soit p proj et s sym, ils sont orthog. Û f sym.

Minimum de distance réalisé par la projection :

O(E) : ens des endom orthog.

fÎ O(E) Û f(B) b.o.n.Û " xÎ E, ||f(x)||=||x||

SO(E)=O⁺(E) (de det = +1) et O^-(E) de det = -1

s sym, s sym orthog. Û autom.orthog.

reflexion : sym ^ / hyperplan retournement : sym ^ / ss ev de dim (n-2)

Matrice orthog. : matrice carrée inversible tq A^-1=t A

AÎ On( R) Û At A=In Û t AA=In

Det(x1,x2,...xn) est le det de ses vect dans une b.o.n.

Dét est une forme n-linéaire alternée

E ev de dim 3, " (u,v)Î E², $ ! wÎ E | " xÎ E, Det(u,vuw)=w.x

w=uÙ v cad " xÎ E, Det(u,v,w)=w.x

(uÙ v)Ù w=(u.w)v-(v.w)u uÙ (vÙ w)=(u.w)v-(u.v)w

Ù n’est pas associatif (ni commutatif).

Si (u,v) libre Þ (u,v,uÙ v) base directe de E

cos q =u.v/(||u|| ||v||) sin q =Det(u,v)/(||u|| ||v||)

Matrices orthog. : avec e ={1,-1} q Î [0,2p ]

SO(E)={r(q ), q Î R}

r(q )or(q ’)=r(q +q ’)

Angle de droites : angle entre 2 vecteurs directeurs calculé à p près.

Soit D er D’ ayant pour angle q , s(D) o s(D’) est une rot d’angle 2q et de centre le pt d’intersection

r(q ) o s(D) : réflexion / dte D’ tq (D,D’)=q /2

s(D) o r(q ) : réflexion / dte D’’ td (D,D’’)=-q /2

Th : E ev eucl de dim 3, " f Î SO(E), sa matrice est de la forme :

Toute réflexion est le produit de 0 ou 2 réflexions.

Tout autom orthog peut s’écrire comme le produit de 1 ou 3 réflexions.

F param., F(t)=W +j (t) i+y (t) j j et y sont les eq paramétriques.

F de cl Ck si j et y sont de cl Ck

r=a (t) et q =b (t) : eq param en polaire

Th. de relèvement : FÎ Ck(I,E) avec k ³ 1 tq " tÎ I,F(t)¹ W

alors $ (a ,b )Î (Ck(I,R))² | F=W +a u o b (ou r=a (t) et q =b (t) tÎ I)

a  : chgmt de param de Ck : fct Ià I1, a bijective, de cl Ck et a ^-1 de cl Ck

Soit F et F’ 2 param. : F~k F’ si $ a chgmt de param tq F=F1 o a (ils sont Ck équivalents et positivement si a st croissante).

~k et ~(k,+) sont des rel. d’equivalence.

Arc géom : classe d’équivalence pour ~k (ou ~(k,+) pour un arc orienté)

G a une ½ tg lorsque tà (F(t)-F(t0))/||F(t)-F(t0)|| a une limite en t0- (tg si en t0- et t0+)

M0 est régulier pour G si F’(t0)¹ 0

il est birégulier si (F’(t0),F’’(t0)) est libre

M0F(t) se décompose localement dans la base (F’(t0),F’’(t0)) avec une ordonnée >0

$ (i,j)Î [[1,k]]² tq (F⁽ⁱ⁾(t0), F^(j)(t0)) est une base de E, i<j (soit p et q ces + petits entiers)

On a le d.l. :

Position de la courbe :

• p impair et q pair : pt d’allure ordinaire
• p et q impairs : point d’inflexion
• p pair et q impair : point de rebroussement de 1^ère espèce
• p et q pairs : point de rebroussement de 2^ème espèce

Recherche pratique de la nature d’un point sur une courbe :

à on calcule les derivées successives de j et y

à on cherche un d.l. de j et y à un ordre suffisant.

Longueur de G  : " F param. [a,b] à E de G

 : abscisse curviligne de M pour l’origine M0(t0)

Param. normalisé de G  : tout param. G :Jà E tq " sÎ J, ||G’(s)||=1

Soit un arc géom de cl Ck (k³ 1) sans pt doubles : il a param normalisés Û pas de pts singuliers.

Repère de Frenet : G un arc géom de cl Ck (k³ 1)

(F(s),t,n) tq t dirigé par la ½ tg en F(s) et qu’il soit o.n. direct

ex : la chaînette (y=ach(x/a))

ellipse, parabole, cycloïde ...

Courbure : G : Jà E normalisé, " s, (F(s),t(s),n(s)) rep de Frenet, $ j  : Jà R tq " sÎ J, t(s)=u(j (s)) et n(s)=u1(j (s))

j (s) est l’angle de contingence de la ½ tg en M(s)

c(s)=j ’(s) est appelé la courbure de G en M(s)

Formules de Frenet : " sÎ J, t’(s)= j ’(s)n(s) et n’(s)=- j ’(s)t(s)

Rayon de courbure : R(s)=1/c(s)

Centre de courbure : W (s)=F(s)+R(s)n(s) (Le cercle de centre W (s) et de rayon R(s) approche le mieux la courbe en M).

à Développée : ens des centres de courbure

a (u) : longueur de l’arc, G param normalisé G=Foa ^-1, t(a (u))=F’(a (u))/a ’(u) et t’(a (u))a ’(u)=(toa )’(u)=c(a (u))n(a (u))a ’(u)

Application à la cinématique

r=f(q ) Û F(q )=W +f(q ).u(q ) avec u(q )=cos q i+sin q j

Si f a une période T : F invariante par rot d’angle T.

f p -périodique à int de longueur p et sym / W

f 2p -périodique à int de longueur 2p (toute la courbe)

" q Î I tq q +p Î I, f(q +p )=-f(q ), f est 2p périod. Et F est p périod.

Vérifier s’il y a des symétries éventuelles

les tg en M0(q 0)=W sont les droites passant par W d’angle polaire q 0

aux autres points : F’(q )=f’(q )u(q )+f(q )u1(q ) avec f(q )¹ 0

Pt d’inflexion lorsque Det(F’(q ),F’’(q )) s’annule en changeant de signe

Branche infinie lorsque f(q )à ± ¥

Courbes classiques :

• cercles de centre W , f(q )=c
• dtes ne passant pas par W , f(q )=-h/(u cos q +v sin q ) (dte verticale : ux=-h)
• cercles passant par W , f(q )=2a cos q +2b sin q
• coniques f(q )=p/(1-e cos q )

Eq générale : r=a/(b+c cos q +d sin q ) (a=0 pt W , c=d=0 : cercle de centre W , b=0 dte ne passant pas par W , a¹ 0, b¹ 0 à conique ).

Dte passant par A(x0,y0) dirigée par u(a ,b ) : b (x-x0)-a (y-y0)=0, orthog à N(u,v)¹ 0, ux+vy+h=0

Eq normalisée :ux+vy+h=0 lorsque u²+v²=1

Cercles d’Appolonius : courbes de niveaux ...

coniques : ens M tq d(F,M)=e d(M,D) Û (1-e²)x²+y²-2epx-p²=0

e=1 parabole, e<1 ellipse, e>1 hyperbole ...

Recherche inverse : Ax²+By²+Cx+Dy+E=0

• AB=0 : parabole
• AB>0 :

1. E’<0 : G =Æ
1. E’=0 : G ={M0}
1. E’>0 : ellipse ¹ point

• AB<0 :

1. E’=0 : hyp. dégénérée en ses 2 asymptotes
2. E’<0 : on peut se ramener à E’>0
3. E’>0 : hyperbole

L’hyperbole est équilatère si les asymptotes sont orthogonales.

Ellipse : f et F’ les 2 foyers " MÎ E, MF+MF’=2a

Hyperbole : |MF’-MF|=2a et réciproquement

Géométrie en dim 3 :

On distingue les surfaces et les courbes

Eq plan : passant par A et dirigé par plan : Vect (U(a ,b ,g ),U’(a ’,b ’,g ’)) (on écrit le déterminant égal à 0)

eq de la forme : ux+vy+wz+h=0 et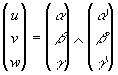

ou eq param. M=A+l U+l ’U’

eq param de dte :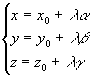

Faisceau de plans :

Soit D une dte d’eq les plans contenant D sont : l Î R

eq de sphère : (x-a)²+(y-b)²+(z-c)²=R²

eq param cercle donné par plan, centre, rayon.

Proj ^ cercle sur plan est une ellipse

Distance dte-point : D : ux+vy+h=0 M0(x0,y0)Î E Þ d(M0,D)=|ux0+vy0+h|/Ö (u²+v²)

dans l’espace : d(M0,D)=|ux0+vy0+wz0+h|/Ö (u²+v²+w²)

dans l’espace : d(M0,D)=||MoAÙ u||/||u||

Angles : (AB,CD)=arg ((d-c)/(b-a))

condition d’alignement : ABC alignés Û (b-a)/(c-a)Î R

condition d’orthogonalité : AB ^ AC Û (d-c)/(b-a)Î iR

condition de cocyclicité : ABCD cocycliques Û (c-a)(d-b)/((d-a)(c-b))Î R

I(f)={MÎ E | f(M)=M}

isométrie : " (M,N)Î E², ||f(M)f(N)||=||MN||

f isom. Û f applic. affine et g (endom. assoc.) est orthogonal.

à SO(E) : isom >0 ou déplacement

à O^-(E) : isom <0 ou antidéplacement

H et H’ 2 hyperplan parallèles s(H’) o s(H)=t(2u) avec t(u)(H)=(H’) et réciproquement

H et H’ 2 hyperplans non parallèles s(H’) o s(H) Î Is⁺(E)

Hyperplan médiateur

en dim 2, rot affine (...)

Dans le plan : Is⁺(E)=TÈ {rot. affines}

Similitudes : d(f(M),f(N))=k.d(M,N)

Si rapport >0 (simil directe) : composées d’isom. et d’homoth. affines de rapport ¹ 0

Th. : décomposition simil directe en rot et homothétie.

$ ! Simil directe | s(A)=A’ et s(B)=B’

en dim 3, O⁺(E)={rot. vectorielles}

rot d’axe D d’angle q pou l’orient de u (conserve D ...)

Vissage : composée d’une rot d’axe D d’angle q pour l’orient de u et d’une translation de vecteur l u

Les isom >0 sont les vissages