 Fractions rationnelles :

à Fractions rationnelles :

R=P/Q avec PÙ Q=1 et Q normalisé : écriture canonique

Pôle de R : racine de son dénominateur

Si deux frac. rationnelles coïncident en une infinité de pts Þ R1=R2

Décomposition en éléments simples :

Q irred normalisé, a Î N*, PÎ K[X], d°(P)<d°(Q) alors $ ! (P1 ... Pa )Î K[X]a tq :

avec " iÎ [[1,a ]], d°(Pi) £ d°(Q(X))

Recherche des parties polaires d’ordre 1 et 2 :

1° R(X)=A/(X-a)+R1(X) ( =P(X)/((X-a)Q1(x)) )

A=P(a)/Q1(a)=P(a)/Q’(a)

2° avec B=P(a)/Q2(a) et P’(a)=AQ2(a)+BQ2’(a)

Méthode :

R canonique, décomposer Q(X)

Trouver les pôles

Pour les parties relatives aux facteurs irréductibles de 2^ème degré : si 2 inconnues multiplier par X et prendre en +¥ sinon, décomposer dans C(X) (utiliser 2^ème point) et recomposer

à Intégration des fractions rationnelles :

Intervalle de recherche

Vérifier si R est de la forme P’/Pa , vérifier que R n’est pas déjà un élément simple

Décomposer en éléments simples

Intégrer terme à terme :

Partie polaire en A/(x-a)a ,primitive en 1/(x-a)a ^-1 ou en ln ...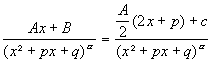

2^ème partie difficile à intégrer

si a =1 : intégr ò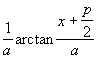

si a ¹ 1 : chgmt de variable u=x+p/2

On effectue une IPP pour trouver une relation de récurrence sur a .

qq chgmt de variables :

Si invariance par xà p -x : u=sin x xà -x : u=cos x xà p +x : u=tan x

Si en sh (x) ou ch(x) : u=exp(x)

si : u=sin t : u=tan t : u=ch t