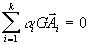
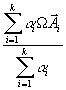
à Propriétés affines des R-espaces vectoriels :
T={t(u),uÎ E} est stable pour o.
M(W ,B)(P)=M(B)( W P)
R’(W ,B) et R’’(W ’,B’) 2 repères posons C=M(R’)(W ’) et P=P(B,B’)
M(R’)(Q)=P*M(R’’)(Q)+C
| Barycentre : $ ! GÎ E | | 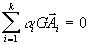 |
" W Î E, G=W + | 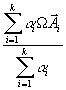 |
Variété affine : A va Û $ F ss ev de E, $ uÎ E | A=t(u)(F)
$ ! Va dirigée par F contenant W
2 va sont parallèles au sens propre si leur directeurs sont égaux et au sens généralisé s’ils sont inclus l’un dans l’autre.
AÌ E, A convexe Û elle est stable par barycentres à coef. positifs. (Toute va et tt segment est convexe).
Applications affines : E Î R-ev, applic affine : Eà E $ j Î L(E) et uÎ E | f=t(u)oj (ils sont uniques).
!!! : F représente une fct et f son endomorphisme associé.
(F(A)F(B))=f(AB) et F(A+u)=F(A)+f(u) (FoG)=f o g
homothétie : h(M)= W +k W M
affinité de base E1 de dir E2 de rapport k p projection sur E1 p à E2, alors " MÎ E, a(M)=p(M)+k p(M)M
à Systèmes d’équations linéaires :
(E) 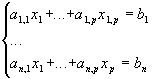
A de t.g. a(i,j) B de t.g. b(i) X de t.g. x(i)
(x1..xn) est sol de (E) Û AX=B
rg(E)=rg(A)
L’ens des sol de (e) est un ss ev de Kp de dim p-r
S est soit vide soit une va dirigée par s
à Un syst de Cramer a une sol unique.
La sol de (E) est (x1...xn) avec " iÎ [[1,n]], xi=det(Ai)/det(A) où Ai est obtenue en remplaçant dans A la i ieme colonne par B.
Méthode du pivot de Gauss :
On peut appliquer des opérations élém. sur un syst. sans changer les sol (suppression d’eq 0=0, échange de 2 eq, echange de la place de 2 inconnues, mult d’une eq par l ¹ 0, ajout à une eq. une c.l. des autres ).
On transforme le système en système pseudo-triangulaire à diagonale partout non nulle.
S’il y a des sol : (x1...xp) sol principales et (x(p+1)...xn) sol paramétrantes.