à Suites réelles ou complexes :
Convergence : $ lÎ C | " e >0, $ N0Î N | " nÎ N, n>N0 Þ |Un-l| £ e
à limite unique
Suites extraite : $ j extractrice | " nÎ N, Vn=U j (n) evac j croissante
Si 2 suites extraites convergent vers des lim. diff. Þ la suite diverge
Passage à la lim. dans une inégalité large : u£ v APCR (A Partir d’un Certain Rang) alors l £ m
Th. des gendarmes et entraînement : u£ v£ w si u et w ont la même lim. p Þ và p ...
Th. : uà pÞ f(Un)à f(p) si f est continue
Th. de la lim. monotone : u croissante APCR Þ lim réelle ou +¥ (lim réelle si u majorée)
Th. des suites adjacentes :
u croissante, v décroissante v-uà 0 Þ u et v convergent vers la même limite et u£ v, Un£ l £ Vn
Th. de Bolzano-Weierstrass :
De toute suite bornée, on peut extaire une suite convergente.
Comparaison de suites :
~ Þ O et o Þ O Il sont seulement compatibles avec le produit.
Changement de variable :
f continue, et j de cl C1 sur le segment
![]()
à Fonctions usuelles :
Dérivée de racine nème : 1/(n(nÖ )n-1)
Fonction ln :
Branche parabolique de direction asymptotique Ox
Fonction exp :
exp(x)/xà +¥ qd xà +¥ x exp(x)à 0 qd xà -¥
(ln x)a /xbà 0 qd xà +¥ xb/eg à 0 qd xà 0
Fcts hyperboliques :
![]()
![]()
sh impaire et ch paire
sh(x)/xà +¥ et ch(x)/xà +¥ qd xà +¥
é les courbes ont une branche parabolique de dir asymptotique Oy.
f x->ex/2 est asymptote aux 2 courbes.
è " x Î R ch²x - sh²x=1
Fcts circulaires réciproques :
" xÎ [-1,1], sin(arcsin(x))=x
" xÎ [-p /2,p /2[, arcsin (sin(x))=x
" xÎ [-1,1], cos(arcsin(x))=Ö (1-x²)
| Arcsin'(x) = | 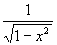 |
Arccos'(x) = - | 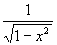 |
Arctan'(x) = | 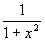 |
" x Î R, tan(arctan(x)) = x " xÎ ]p /2,p /2[, arctan(tan(x)) = x
" x>0, arctan(1/x)=p /2-arctan(x)
à Comparaison de fonctions :
Il n’y a pas compatibilité pour l’addition
... mais si f=O(h) et g=O(h) Þ f+g=O(h)
f=o(h) et g=o(h) Þ f+g=o(h)
On n’a pas stabilité par une fonction qcq.
à Développements limités :
d.l. de la forme, si x0Î R, f(x)=a0+a1(x-x0)+a2(x-x0)²+ ... +an(x-x0)n+o((x-x0)n)
si x0=± ¥ f(x)=a0+a1/x+a2/x²+ ... +an/xn+o(1/xn)
Th. d’intégration
Principe de troncature : avec un dl à l’ordre n on peut en avoir un autre à l’ordre p<n (avec un nouveau petit o).
Th. de Taylor Young :
![]()
règle pour produit : on conserve le plus petit (petit o).
règle pour la composition : ne pas oublier de calculer le petit o de la fct composée et vérifier que la fonction tend vers 0 en 0.